Cálculo fraccionario: herramienta de la ciencia

Por Érika Rodríguez

Zacatecas, Zacatecas. 27 de octubre de 2016 (Agencia Informativa Conacyt).- El cálculo fraccionario (CF) es una rama de las matemáticas que involucra operadores diferenciales e integrales de orden no entero y es una generalización natural del cálculo ordinario. El CF es una disciplina tan antigua como el cálculo ordinario y ha tenido un repunte mundial en los últimos 40 años, debido a los resultados en la explicación de la difusión anómala y otros procesos físicos y biológicos.

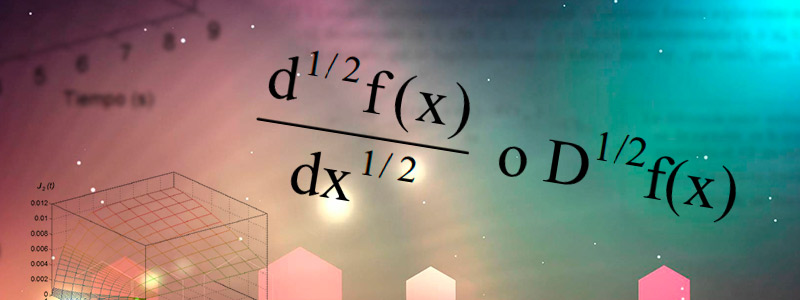
En la naturaleza existe una infinidad de fenómenos que tienen una descripción fraccionaria intrínseca y, por consiguiente, es necesario usar el CF para dar una explicación correcta, expresó en entrevista el doctor Juan Rosales García, profesor investigador de la División de Ingenierías Campus Irapuato-Salamanca de la Universidad de Guanajuato (DICIS Ugto).

“Hoy en día, en México no existen grupos consolidados en el estudio y aplicación del cálculo fraccionario; sin embargo, hay quienes de manera aislada desarrollan proyectos de investigación usando esta herramienta”, puntualizó el doctor Rosales García.

Con el objetivo de difundir las aplicaciones del cálculo fraccionario, investigadores, especialistas, docentes y estudiantes, en su mayoría de licenciatura y posgrado, se dieron cita del 12 al 16 de septiembre de 2016 para exponer y discutir los resultados de sus investigaciones y futuros proyectos en el Third Mexican Workshop on Fractional Calculus, en la Unidad Profesional Interdisciplinaria de Ingeniería, Campus Zacatecas del Instituto Politécnico Nacional (UPIIZ IPN).

Juan Rosales García.Rosales García, cofundador de estos eventos, informó que el objetivo de los workshops es difundir la importancia que tiene el CF en la descripción de los fenómenos naturales y las aplicaciones a las ingenierías, atraer la atención de investigadores, docentes y estudiantes para poder formar grupos sólidos de investigación en nuestro país.

“Este es un evento bianual en el que participantes de México y de otros países exponen los resultados de sus investigaciones y proyectos basados en el cálculo fraccionario. Las instituciones que establecieron estos eventos desde su fundación en 2012, son la DICIS Ugto, donde se realizaron los dos primeros workshops, y la Unidad Académica de Matemáticas de la Universidad Autónoma de Zacatecas (UAM-UAZ). En esta ocasión, se incorporaron como parte del comité nacional la UPIIZ IPN y el Instituto Tecnológico Superior de Jerez (ITSJ) —que forma parte del Tecnológico Nacional de México (Tecnm)—”, describió la doctora Leticia Adriana Ramírez Hernández, directora de la UAM-UAZ.

Expresó que el comité internacional del evento referido desde sus inicios ha sido encabezado por el doctor Juan Rosales García, profesor investigador de la DICIS Ugto, y ha tenido como invitado especial, en cada ocasión, al profesor Dumitru Baleanu, investigador del Instituto de Ciencias del Espacio, Bucarest-Magurele, Rumania, considerado un líder mundial en el cálculo fraccionario y sus aplicaciones. El profesor Baleanu cuenta con aproximadamente cinco mil citas tipo A y está entre los 100 investigadores más citados del mundo en 2015 y 2016. 

En esta ocasión, se brindó un curso de cinco horas impartido por el mundialmente reconocido investigador de la Technical University of Kosice, Eslovaquia, Igor Podlubny, líder internacional en el área del cálculo fraccionario, quien ha hecho grandes contribuciones en esta área. Como ejemplo se tiene su libro de Ecuaciones diferenciales fraccionarias, que cuenta con aproximadamente 10 mil citas; sus trabajos en aplicaciones de esta herramienta matemática le dan otras 10 mil citas. 

Entre los exponentes hubo participación del doctor Haret Rosú y Jessica Mendiola, del Instituto Potosino de Investigación Científica y Tecnológica (Ipicyt); Benito F. Martínez, Francisco A. Godínez y Carlos A. Torres, de la Universidad Nacional Autónoma de México (UNAM); Moisés Soto, de la Benemérita Universidad Autónoma de Puebla (BUAP); Jesús Escalante, de la Facultad de Ingeniería Mecánica y Eléctrica (FIME), de la Universidad Veracruzana (UV); Rafael Martínez, del Centro de Investigación y de Estudios Avanzados (Cinvestav) del IPN; Abraham Contreras y Leonardo Martínez, de la DICIS Ugto; José S. Murguía, de la Universidad Autónoma de San Luis Potosí (UASLP), detalló la doctora Ramírez Hernández.

Proyectos en México basados en cálculo fraccionario

Rosales García, también miembro nivel I del Sistema Nacional de Investigadores (SNI) del Consejo Nacional de Ciencia y Tecnología (Conacyt), expresó que actualmente se encuentra desarrollando dos proyectos con base en el cálculo fraccionario. Uno de ellos consiste en la modelación de pulsos ultracortos —láseres— para aplicaciones en procesos biológicos y el otro en el procesamiento de imágenes médicas.

Por su parte, el investigador del Ipicyt y miembro nivel III del SNI, Haret Rosú, notificó en entrevista que su línea de investigación consiste en el manejo y aplicación de técnicas matemáticas sencillas en diversos campos de la física.

“Conocer los proyectos basados en cálculo fraccionario me ayuda a averiguar si se puede hacer algo desde otro punto de vista. Conozco muy bien la parte matemática, pero al aplicar otro método de cálculo quizá pueda resultar algo novedoso, es lo que busco”, expresó el físico teórico y matemático.

Otro de los trabajos presentados en el evento consiste en el análisis de la transferencia de masa y calor, utilizando los conceptos del cálculo fraccionario. Esta exposición estuvo a cargo del doctor en ingeniería Francisco Godínez, académico de la Facultad de Ingeniería de la UNAM.

“En mi más reciente publicación basada en cálculo fraccionario, trabajé con procesos de conducción electromagnética en medios porosos. Tengo algunos otros desarrollos; por ejemplo, ahora estoy trabajando en el diseño de una suspensión magnética y en el desarrollo de robots para emular el nado de bacterias, desde el punto de vista hidrodinámico”, relató el doctor Godínez, quien es miembro nivel I del SNI.

Geometría fractal con el cálculo fraccionario

El doctor en matemáticas Moisés Soto refirió en entrevista su reciente participación en la investigación del Departamento de Matemáticas de la UNAM, en donde se busca relacionar la geometría fractal con el cálculo fraccionario. El proyecto es encabezado por el doctor Fernando Brambila Paz.

“La idea es hacer una aportación e investigación general para relacionar la geometría fractal con el cálculo fraccionario. Se trata de dos áreas del conocimiento distintas, pero desde hace algunas décadas esa relación ha atraído a investigadores de prestigio internacional. Ya hay evidencias de que estas dos áreas se relacionan, pero todavía no están muy claras desde el punto de vista matemático formal. Todavía no es definitivo, pero es una aportación importante”.

Reveló que este trabajo consiste en formalizar matemáticamente la relación entre ambas áreas. Asimismo, informó que ha sido respaldado por la Asociación Mexicana para la Innovación en Tecnología Educativa, A.C. (AMITE), quienes proporcionaron los recursos para la realización de este proyecto.

Finalmente, el doctor Juan Rosales expresó su intención por incrementar la participación de especialistas de talla mundial para su próxima edición, en el 2018, que posiblemente será en San Luis Potosí o en Guanajuato.